Article Number: 99 | VC6 | VC5 | VC4 | VC3 | Post Date: September 2, 2020 | Updated: June 29, 2022
How is the turning radius of my vehicle related to the steering angle sequence input?
In the case of steering types “front” (the default for all vehicles), “back”, and “front and back” Virtual CRASH uses an Ackerman angle calculation to determine the angle of the wheels at the axle. The "steering angle" input value is the center-line equivalent steering angle, which is used to calculate the inner and outer wheel angles. This is described in more detail below.
In the figure below, we see our vehicle with wheelbase = \(WB\) (distance from points \(a\) to \(e\)) and trackwidth = \(TW\) (distance from points \(a\) to \(c\)). Using either the sequences menu or the fast control icons, you will input a steering angle \(\theta\). Suppose we have a unit vector sitting at point \(b\) on the centerline of our vehicle (gray line below), with angle \(\theta\) with respect to the vehicle’s local \(x\)-axis. We can imagine a line orthogonal to this vector, which intersects with an imaginary line running through the centers of the rear wheels (points \(e\) and \(d\)). This intersection point is the center of rotation for our vehicle’s turning motion (point \(O\)). Let’s define the vector \(\vec{r}\) that extends from point \(O\) to point b. Let’s now imagine another vector, \(\vec{r}_o\), that extends from point \(O\) to center of the outer wheel (point \(a\)). We can solve for unit vector orthogonal to \(\vec{r}_0\). This unit vector will have an angle \(\theta_o\) relative to the vehicle’s local \(x\)-axis. Our outer wheel will point in the direction of this unit vector. Finally, suppose we extend a vector, \(\vec{r}_i\), from the point \(O\) to the center of the inner wheel (point c). We can again solve for the unit vector that is orthogonal to \(\vec{r}_{i}\). The unit vector will have an angle \(\theta_{i}\) with respect to the vehicle’s local \(x\)-axis. Our inner wheel will point in the direction of this unit vector. With a fixed steering angle \(\theta\), in the quasi-static limit with no slip, we expect our wheel centers to remain at fixed radii relative to the center of rotation throughout the turning maneuver. The outer steering radius (curb to curb radius excluding the half tire width distance) is given by \(|\vec{r}_{o}|\).
Since by construction, the unit vector at point \(b\) is orthogonal to \(\vec{r}\), we know the angle between the line connecting points \(a\) and \(c\) and \(\vec{r}\) is \(\theta\).
Let’s assume the center of rotation is at \( (x,y) = (0,0) \). This implies the \(x\) coordinate for point b is given by \(WB\) and the \(y\) value by \( {WB \over \tan\theta} \).
Thus,
$$\vec{r} = (WB, {WB \over \tan\theta}) $$
Similarly, the outer steering radius vector is given by:
$$\vec{r}_{o} = (WB, {WB \over \tan\theta} + {TW \over 2}) $$
Finally, the inner steering radius vector is given by:
$$\vec{r}_{i} = (WB, {WB \over \tan\theta} - {TW \over 2}) $$
The magnitude of the outer steering radius (curb to curb radius excluding the half tire width distance) is given by:
$$|\vec{r}_{o}| = \sqrt{WB^2 + ({WB \over \tan\theta} + {TW \over 2})^2} $$
We can easily make a spreadsheet to explore various outer radii as a function of \(\theta\) (steering angle). This is shown below for our test vehicle:
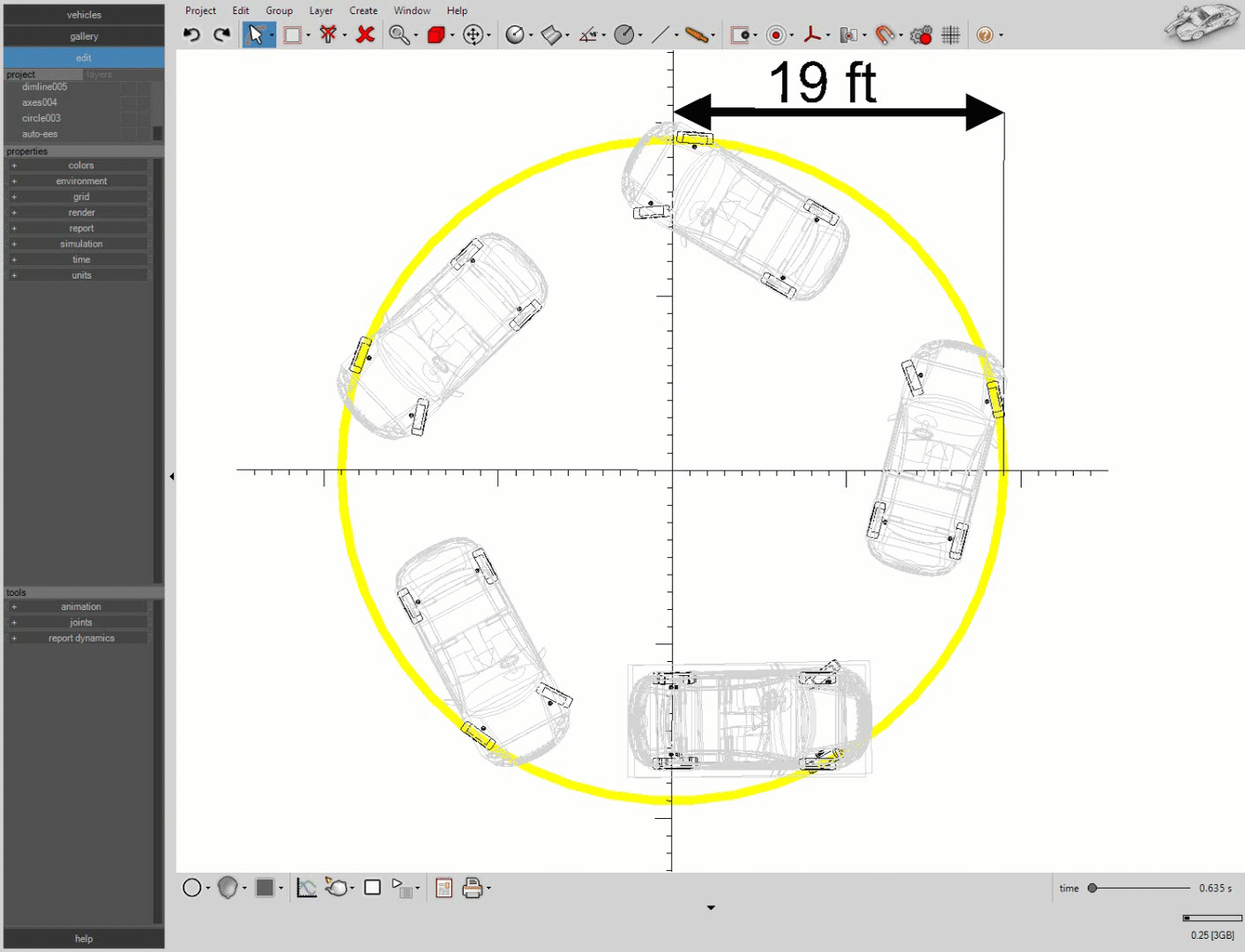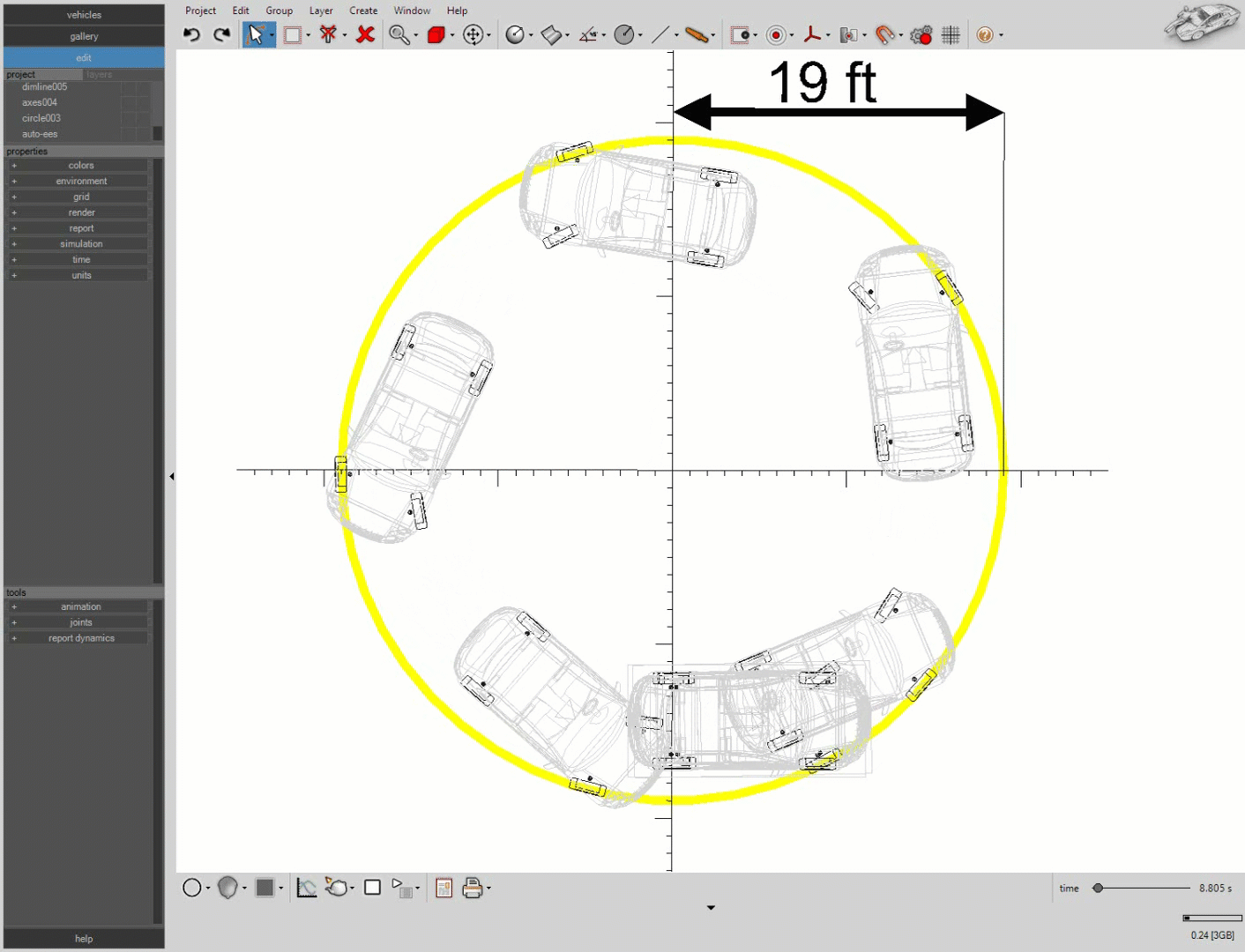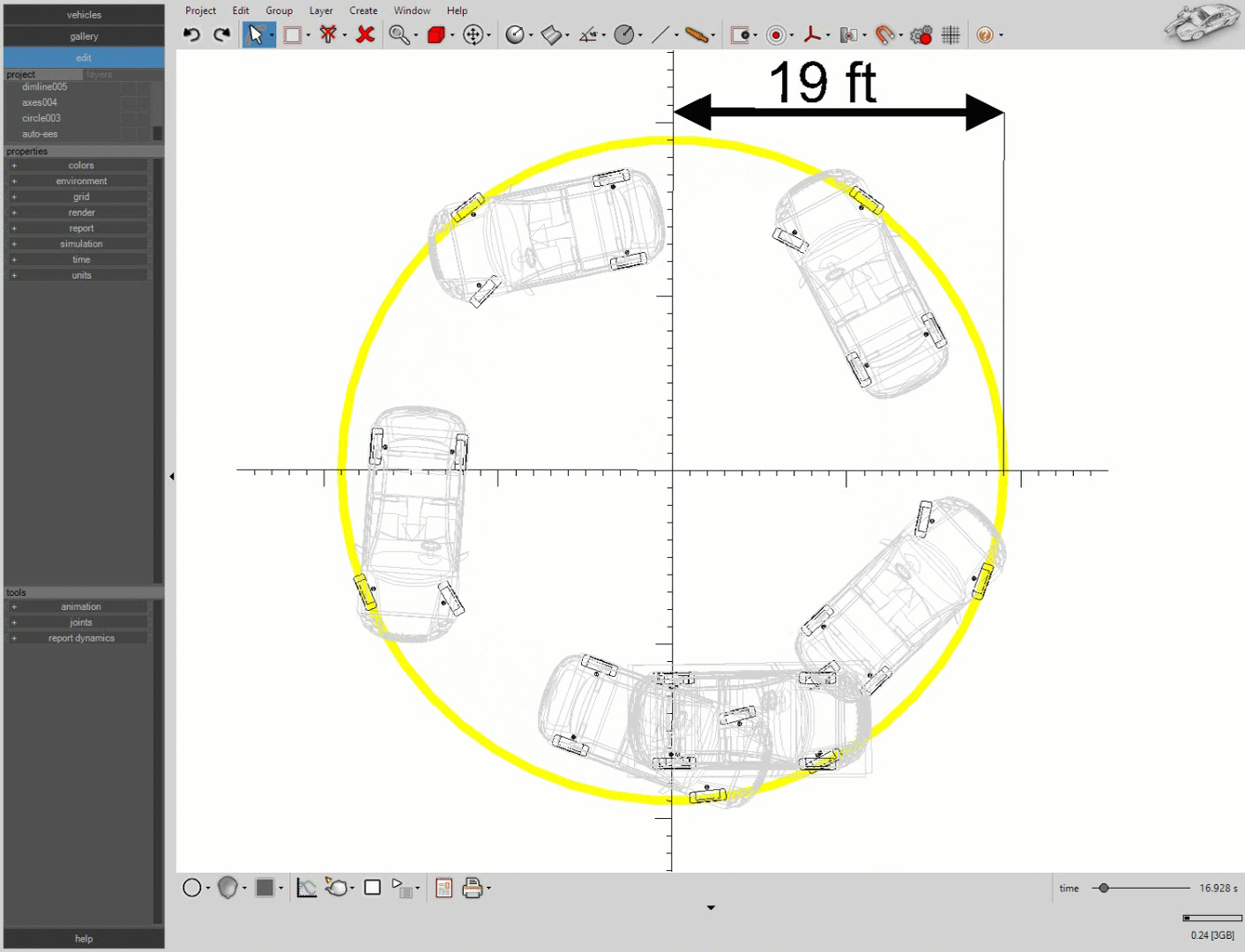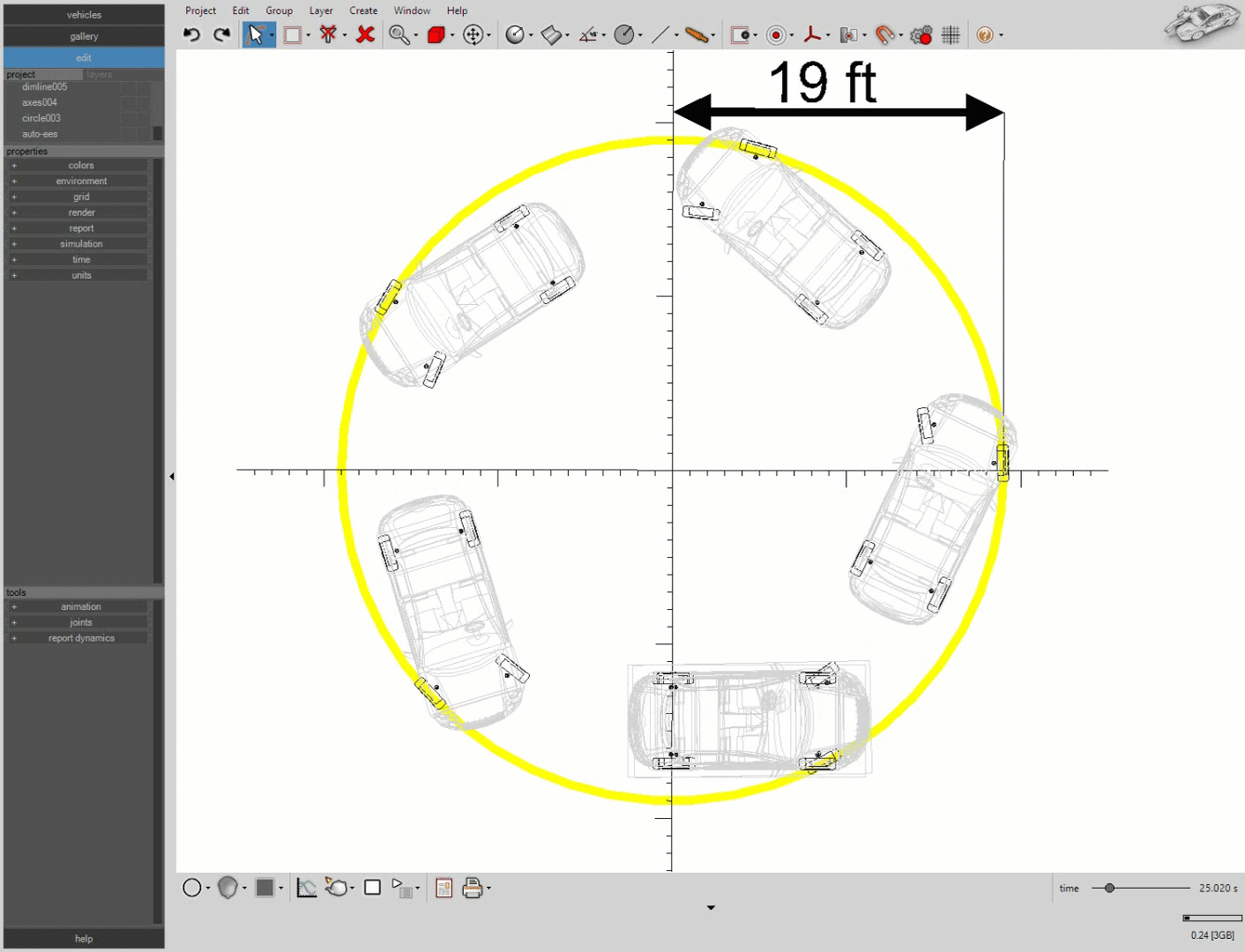
A simulation of our vehicle steering with a 30 degree initial steering angle is shown below. Notice, the 19 ft radius circle in yellow.
Relating \(\theta_o\) and \(\theta_i\) to \(\theta\)
Inner radius
One can easily solve for the relation between \(\theta_o\) and \(\theta_i\) to \(\theta\). Let’s assume a unit vector \(\vec{u}_i = (u_{i,x}, u_{i,y})\) sits at point \(c\). Let’s assume this vector is orthogonal to \(\vec{r}_{i}\). That is:
$$ \vec{u}_i \cdot \vec{r}_{i} = u_{i,x} \cdot WB + u_{i,y} \cdot ({WB \over \tan\theta} - {TW \over 2}) = 0 $$
Therefore:
$$ -{ u_{i,y} \over u_{i,x} } = { WB \over {WB \over \tan\theta} - {TW \over 2} } $$
That is, \(\theta_i\) is related to \(\theta\) by:
$$\tan\theta_i = { WB \over {WB \over \tan\theta} - {TW \over 2} } $$
or
$$ \theta_i = \tan^{-1}({ WB \over {WB \over \tan|\theta|} - {TW \over 2} }) \cdot sign(\theta) $$
Outer radius
Next let’s assume a unit vector \(\vec{u}_o = (u_{o,x}, u_{o,y})\) sits at point \(a\). Let’s assume this vector is orthogonal to \(\vec{r}_{o}\). That is:
$$ \vec{u}_o \cdot \vec{r}_{o} = u_{o,x} \cdot WB + u_{o,y} \cdot ({WB \over \tan\theta} + {TW \over 2}) = 0 $$
Therefore:
$$ -{ u_{o,y} \over u_{o,x} } = { WB \over {WB \over \tan\theta} + {TW \over 2} } $$
That is, \(\theta_o\) is related to \(\theta\) by:
$$\tan\theta_o = { WB \over {WB \over \tan\theta} + {TW \over 2} } $$
or
$$ \theta_o = \tan^{-1}({ WB \over {WB \over \tan|\theta|} + {TW \over 2} }) \cdot sign(\theta) $$
Tags: Steering angle, inner radius, outer radius, turning radius, curb to curb, Ackerman angle.
© 2021 Virtual CRASH, LLC. All Rights Reserved